Simulation numérique de rendu d’un trou noir.
(Crédits: BlackRainbow sur Blenderartists)

Si vous avez lu la première partie de l’article consacré aux trous noirs, vous avez pu vous familiariser avec ces objets chers aux auteurs de science-fiction. Si vous ne l’avez pas lu, je vous conseille fortement d’y jeter un œil avant de continuer, car maintenant je vous propose d’approfondir un peu et de découvrir les différents types de trous noirs.

Ceux qui n’existent que sur le papier, et ceux qui sont là quelque part…

Nous verrons aussi ce à quoi serait confronté un explorateur qui souhaiterait s’y aventurer, et comment, peut-être un jour, nous pourrions les utiliser pour voyager…

Les quatre types de trous noirs

Nous avons vu dans la première partie qu’il suffisait de trois paramètres pour décrire un trou noir: Sa masse, son moment angulaire (rotation) et sa charge électrique. Concernant sa masse, nous avons vu qu’il pouvait exister des trous noirs stellaires, reliquats de la mort d’une étoile massive, et des trous noirs supermassifs (d’origine encore indéterminée à ce jour) comme l’on peut en trouver dans les centres des galaxies. Bien que ce ne soit apparemment pas systématique.

Ici nous allons voir les différents types de trous noirs en jouant sur les deux autres paramètres, et découvrir leurs effets.

Trou noir de Schwarzschild

Karl Schwarzschild

Sans aucun doute le plus simple, puisqu’il s’agit d’un trou noir de charge nulle et de moment angulaire nul, c’est à dire qu’il ne tourne pas. Alors ? A-t-on une chance d’en trouver un dans l’univers ?

Lorsqu’un trou noir stellaire se forme, il hérite des deux paramètres de l’étoile qui l’a engendré. Il faudrait donc, pour cela, trouver une étoile de charge nulle et qui ne soit pas en rotation… Autant dire qu’il est quasiment impossible que ce type de trou noir existe réellement. Alors d’où sort-il ? Me direz-vous. Et bien du cerveau de Karl Schwarzschild.

Ce dernier à fortement contribué à la théorie des trous noirs en utilisant la toute récente (à l’époque) équation du champ d’Einstein. Il en prit connaissance alors qu’il était enrôlé sur le front russe de la 1ère guerre mondiale.

Rassurez-vous, nous n’allons pas décrire cette formule. En appliquant cette théorie à une étoile sphérique et immobile pour une question de simplicité de calcul, Schwarzschild a mis en évidence l’existence probable des trous noirs.

Ce trou noir est donc une solution mathématique de l’équation du champ d’Einstein. Et il est fortement improbable qu’il puisse en exister un quelque part dans l’univers.

Il est à noter que, de part sa géométrie et son absence de rotation, un trou noir de Schwarzschild ne possède pas d’ergosphère. Celle-ci est confondue avec l’horizon des événements, et sa singularité est ponctuelle. C’est à dire qu’il s’agit d’un minuscule point de l’espace.

Trou noir de Reissner-Nordström

Gunnar Nordström & Hans Reissner

Peu de temps après la découverte de Schwarzschild, deux scientifiques trouvèrent la solution dans le cas d’un trou noir sans moment angulaire mais qui possèderait une charge électrique. Il s’agit de Hans Reissner et Gunnar Nordström.

Ceux-ci trouvèrent cette solution de l’équation du champ d’Einstein et montrèrent que dans ce cas là, il n’existait plus un mais deux horizons appelés « intérieur » et « extérieur ». Lorsque l’on franchi le premier horizon le temps et l’espace prennent la place de l’autre. C’est à dire que le déplacement vers l’avant va se transformer en déplacement vers le futur, il sera donc impossible de s’arrêter. Puis le franchissement du deuxième horizon va ré-inverser l’espace et le temps, rétablissant la situation. Il sera donc possible de naviguer librement à l’intérieur du 2ème horizon et, même, d’éviter la singularité.

A mesure que la charge du trou noir augmente, les deux horizons vont se rapprocher. S’ils se confondent, ils vont s’annuler et disparaitre.

Ce qui reviendrait à dire que la singularité pourrait exister nue (ponctuelle). C’est à dire qu’elle pourrait être dépourvue d’horizon des événements.

Or ceci entre en contradiction avec le principe de censure cosmique de Robert Penrose, qui dit (en gros) qu’il est impossible qu’une singularité gravitationnelle ne puisse exister sans horizon des événements, car cela permettrait à la singularité (dont le comportement est incompatible avec les lois de la physique actuelle) d’influer sur notre univers.

Ceci tendrait à dire qu’un trou noir de ce type ne pourrait pas exister dans la nature.

Trou noir de Kerr

On appelle trou noir de Kerr, un trou noir qui possède un moment angulaire mais pas de charge électrique. C’est le mathématicien néo-zélandais Roy Kerr qui trouva cette solution en 1963.

Le professeur Roy Kerr

Ceci créé trois différences majeures par rapport à celui de Schwarzschild:

• Sa singularité est annulaire c’est à dire qu’elle possède la géométrie d’un tore
• Il possède deux horizons
• Il possède une ergosphère

Nous avons vu qu’un trou noir héritait du moment angulaire de l’étoile qui l’a créé. C’est à dire qu’il va garder la même vitesse de rotation que cette étoile. Ce qui implique une dépense en énergie cinétique pour le trou noir.

Cette rotation va emporter avec elle une partie de l’espace, c’est ce que l’on appelle l’ergosphère.

Toute matière qui franchira la limite de l’ergosphère aura la possibilité de gagner de l’énergie cinétique en embrassant la rotation de l’espace. Ce qui veut dire que si cette matière parvient à quitter l’ergosphère, elle aura « volé » de l’énergie au trou noir.

De leur coté, les deux horizons permettent d’approcher la singularité et même de l’éviter, puisque, à l’instar du trou noir de Reissner-Nordström, le franchissement du deuxième horizon va ré-inverser l’espace et le temps.

De plus, de la même façon que le précédent, plus le moment angulaire est important (donc plus le trou noir tourne vite), et plus les deux horizons se rapprochent.

Trou noir de Kerr-Newman

Ezra Ted Newman

Il s’agit de la solution la plus générale à l’équation de champ d’Einstein, puisqu’elle décrit un trou noir possédant un moment angulaire ET une charge électrique, bien qu’il semble peu probable qu’une étoile soit très fortement chargée dans la nature.

Formulée par Ezra Ted Newman en 1965 et reprenant comme base la solution de Roy Kerr, cette solution ne remet pas en cause la description fournie par ce dernier pour son trou noir en rotation, mais elle en est un complément.

Explorer un trou noir

Pour cette phase d’exploration, nous allons considérer que le trou noir que l’on va visiter sera de type « Kerr », c’est à dire en rotation et avec une charge électrique nulle ou négligeable.

Cas du trou noir stellaire

Le trou noir stellaire Cygnus X1 de 8,7 masses solaires observé en rayons X.
(Crédits: NASA)

Un trou noir stellaire, est le résultat de la mort et de l’explosion d’une étoile massive ou supermassive en supernova. Il s’agit des plus « petits » trous noirs stables que l’on connaisse.

Que se passerait-il si l’on essayait de s’en approcher ?

Admettons que deux navettes soient chargées de son exploration, l’une « A » devant franchir l’horizon et l’autre « B » rester à l’écart afin d’observer ce qu’il se passe.

A entame sa descente, et progresse en ligne droite vers l’horizon des événements. Soudain B voit le vaisseau A commencer à tourner autour du trou noir, alors qu’aucune manœuvre n’a été effectuée dans ce sens. Il vient de franchir l’ergosphère, il lui est alors impossible de se stabiliser car l’espace lui-même est en rotation. Mais qu’importe, A continue sa mission.

B le voit s’approcher petit à petit de l’horizon des événements, mais plus il s’en approche, plus il le voit ralentir. Pour A, en revanche, il ne ressent aucun changement, et continue à avancer. Mais, alors qu’il s’apprêtait à franchir l’horizon, le vaisseau est disloqué par les intenses marées gravitationnelles provoquées par la singularité qui s’y cache. A n’est plus qu’un nuage d’atomes, et ses occupants n’y survivrons pas.

B observe la scène à bonne distance et voit toujours A, bien entier, qui semble s’être arrêté.

En réalité, les effets de dilatation du temps deviennent si important au voisinage d’un trou noir, que le temps s’écoule bien plus lentement pour A. Et tous les occupants de B seront morts de vieillesse bien avant qu’ils ne puissent voir le vaisseau A donner des signes d’avaries.

Cas du trou noir supermassif

Noyau de la galaxie NGC 4261 dans la constellation de la Vierge, contenant un trou noir de 400 millions de masses solaires.
(Crédits: NASA/Hubble)

Nous ne savons pas vraiment d’où viennent les trous noirs supermassifs. Leur origine reste encore un mystère, mais nous savons en revanche qu’ils se nichent très souvent au centre des galaxies. Comme c’est le cas de NGC 4261 que nous allons tenter d’explorer.

Le rayon de l’horizon des événements croit avec la masse du trou noir. Or ici la masse est telle, que l’horizon se trouve à plusieurs milliards de kilomètres de sa singularité.

De ce fait, les effets de marée seront inexistants lorsque A franchira l’horizon. Tout ce que verrons ses occupants sera un rétrécissement de la voute céleste. Comment ça ?

Et bien d’après le physicien Kip Thorne, la sphère noire que verraient les astronautes devant eux viendrait les englober. C’est à dire que s’ils regardaient derrière eux, ils ne verraient qu’un cercle se rétrécissant de plus en plus et qui contiendrait la totalité des étoiles (à 360°) qui étaient visible lors de leur entrée.

Dur à imaginer n’est-ce pas ? Et ensuite ?

Ensuite, ils vont devoir parcourir une grande distance à l’intérieur de l’horizon, sans possibilité de s’arrêter ou de faire demi-tour, avant de commencer à ressentir les effets de marée de la singularité. Et finiront-ils pulvérisés ? Il y a de fortes chances oui. Car même si la théorie explique que dans un espace théorique (c’est à dire totalement vide), ils pourraient franchir l’horizon intérieur et naviguer librement, il est fort peu probable qu’ils puissent résister aux marées gravitationnelles de la singularité avant de le franchir. C’est à nouveau une différence entre théorie et réalité, et personne n’est aujourd’hui en mesure de dire ce qu’il adviendrait réellement du vaisseau A.

Le cas du trou de ver

Il est aussi appelé pont de Einstein-Rosen, expression démocratisé par la série américaine Sliders qui contait les aventures d’un petit groupe de personnes perdues dans des univers parallèles auxquels elles accédaient via un trou de ver.

Quant aux lecteurs de mon roman, ils auront pu y voir une approche assez différente, mais basée sur les théories scientifiques qui vont suivre.

Bien sûr cela est de la fiction, et il est actuellement impossible de fabriquer un trou de ver qui soit suffisamment stable pour y faire passer un être humain.

Nous avons vu que la structure de l’univers pouvait être courbée. Un trou de ver serait un raccourci, qui permettrait de passer d’un univers à un autre (dans le cas des univers parallèles), ou d’un point à un autre au sein du même univers. Son nom vient d’une représentation simple de son principe:

Imaginons que l’univers soit une pomme, que vous vous trouviez au dessus de la pomme (A) et que vous vouliez rejoindre le bas (B). Le trajet normal que vous devriez emprunter serait d’en faire le tour. Mais il y a un moyen de faire plus court ! Si vous percez un trou au centre de la pomme, comme le ferai un ver, vous atteindrez le point B beaucoup plus vite.

Illustration du principe du trou de ver.
(Crédit: C.P. Rigel)

D’autres représentations, plus concrètes, montreraient l’espace-temps comme une feuille en deux dimensions que l’on replierait sur elle-même. Le trou de ver serait alors un passage d’une partie de cette feuille vers une autre plus lointaine.

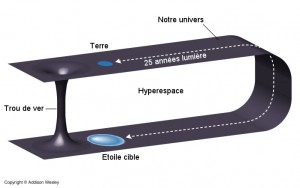
(Crédit: Addison Wesley)

Que dit la science à ce sujet ? C’est ce que nous allons voir.

La science et les trous de ver

Les trous de vers sont plus des solutions mathématique que des objets tangibles. Ce qui pousse les scientifique à douter de leur existence à l’état naturel. Cela dit, il n’est pas exclu que l’on puisse en fabriquer artificiellement.

Trois types distincts de trous de vers sont mathématiquement possibles, et leurs effets sont différents :

• Trou de ver de Schwarzschild: Il découle du trou noir du même nom mais il est absolument infranchissable. La singularité étant ponctuelle, tout voyageur finirait par s’y écraser.

• Trou de ver de Reissner-Nordström: Franchissable, mais dans un seul sens, il ne serait donc pas possible pour un voyageur ou même des photons d’y passer dans l’autre sens.
• Trou de ver de Lorentz: Il a la particularité d’être chargé négativement, et serait franchissable dans les deux sens.

C’est bien évidemment ce dernier type de trou de ver qui serait le plus intéressant. Il ne peut exister à l’état stable que si on lui fourni suffisamment de matière exotique (de masse négative). Seule capable d’appliquer une résistance opposée à la gravité et de stabiliser le passage.

Il serait donc possible de se servir d’un trou noir pour fabriquer un trou de ver en lui injectant de la matière de masse négative.

Mais la science fait face à un autre problème. Le fait que se déplacer dans l’espace-temps, c’est se déplacer dans l’espace mais aussi dans le temps. Et le principe de causalité interdit formellement de voyager dans le passé en stipulant qu’un effet ne peut précéder sa cause.

Ma conception du trou de ver

Dans mon roman, je ne décris pas l’univers de façon lisse et stable. Mais plutôt comme un drap agité par les fluctuations quantiques aussi bien à grande échelle, qu’à l’échelle atomique. La matière exotique que j’ai utilisé pour maintenir le passage est de l’antimatière. Je fais donc une hypothèse comme quoi la masse de l’antimatière pourrait-être négative, suivant par ce biais, l’hypothèse et les travaux de Gabriel Chardin, un physicien français.

Illustration d’un trou de ver dans un espace-temps complexe.
(Crédit: Jacob Feisley)

Enfin, mon approche fut plus prudente que ce que l’on peut voir dans Sliders ou Contact (roman de Carl Sagan) par exemple, où le voyage à lieu depuis la surface de la Terre.

La Terre est constamment en mouvement, autour du Soleil et tournant sur elle-même. Il me semblait improbable d’obtenir une précision assez importante pour calculer l’endroit exact du retour. Il faudrait pour cela calculer la position de la Terre à cet instant précis, ainsi que la position de la sortie du passage sur sa surface. Sans cela, le voyageur risquerait de réapparaître à 2000 mètres d’altitude, 6 pieds sous terre, ou même sur orbite, puisque entre-temps la Terre se serait déplacée…